이번 포스팅에서는 Bayesian의 중요한 토픽인 Variational Inference부터 그와 연관된 Variational Auto-encoder까지 알아보려고 한다.

Bayesian Framework

먼저, 베이지안의 기본적인 사고방식부터 알고 가자. 빈도론자와 베이지안의 가장 큰 차이점은 우리가 추정하고자하는 parameter를 확률변수로 보냐/아니냐이다. 빈도론자는 고정된 상수라고 보고 베이지안은 어떤 확률분포를 따르는 확률변수라고 생각한다.

예를 들어, 우리나라 사람들의 키를 수집한 데이터가 있다고 가정하자. 아무래도 우리가 관심있어 하는 parameter는 우리나라 사람들의 평균 키일 것이다. 빈도론자들은 이 평균 키($\mu$라고 하자.)가 고정된 상수(ex: 168cm)라고 가정하고 ML 방식으로 모수를 추정한다. 그에 비해, 베이지안은 $\mu$에 대한 사전 분포를 먼저 정의한 후(이를 prior belief라고 한다.) 주어진 데이터로 부터 사후분포를 추정한다.

우리나라 사람들의 평균 키가 매우 작다고 믿는 베이지안은 평균이 160cm인 정규분포를 사전분포로 가정할 것이다. 그런데 데이터에 180cm 이상인 사람들이 많다면 데이터를 본 이후 사후분포는 평균이 175cm 정도인 정규분포가 된다. 한편, 빈도론자는 평균 키는 185cm구나!라고 결론을 지을 것이다.

글이 길어졌는데, 여튼 베이지안의 핵심은 데이터에 사전믿음을 결합한다는 것에 있다.

우리가 추정하고자 하는 모수를 $\theta$, 데이터를 $x$라고 할 때 결국 베이지안의 목표는 사전분포 + 데이터로부터 사후분포를 추론하는 것이다. 즉, 다음과 같다.

$p(\theta\vert X) = \frac{\prod_{i=1}^{n}{p(x_{i}\vert\theta)p(\theta)}}{\int {\prod_{i=1}^{n}{p(x_{i}\vert\theta)p(\theta)d\theta}}} \text{ where } x_{i}’s \text{ are i.i.d samples}$

그럼 이제 본격적으로 베이지안 입장에서 본 머신러닝 모델에 대해서 이야기해보도록 하자. $x$를 features, $y$를 class label/latent vector, $\theta$를 추정할 parameter로 정의하겠다. 그렇다면 우리가 관심있는 분포는 $x$가 given일 때 $y, \theta$의 결합 분포에 해당한다.

• $p(y, \theta \vert x) = p(y \vert \theta, x)p(\theta) \text{ } \because x \perp\theta$
• $p(\theta \vert X, Y) = \frac{p(Y \vert X, \theta)p(\theta)}{\int p(Y \vert X, \theta)p(\theta)}\text{ where X, Y denote whole training set}$
• test: $p(y \vert x, X, Y) = \int{ p(y \vert x, \theta)p(\theta \vert X, Y)d\theta}$

그러나 바로 여기에서 문제가 생긴다. $p(\theta \vert X, Y)$를 구하기 위해서는 분모에 있는 적분이 가능해야 하는데, $p(y \vert x, \theta)$와 $p(\theta)$가 conjugate하지 않으면 대부분의 경우에서 적분이 어렵다는 것. test시에도 마찬가지.

(conjugate prior: conjugacy에 대해서는 자세히 언급하지 않겠지만, 궁금하신 분들은 이 링크를 참조하길 바란다. 대표적인 conjugate distributions은 beta-binom, poission-gamma 등이 있다.)

여튼, conjugacy가 없다면 posterior distribution(사후분포)을 구하기가 매우 힘들고 빈도론자들 처럼 $\theta$에 대한 point estimation을 할 수 밖에 없다. 이 경우를 Poor Bayes라고도 한다고… test시에도 이러한 point estimation을 통해 얻어진 $\theta_{MP}$를 가지고 $y$에 대한 추론을 하게 된다.

• $\theta_{MP} = argmax_{\theta}p(\theta \vert X, Y) = argmax_{\theta}P(Y \vert X, \theta)p(\theta)$
• $p(y \vert x, X, Y) \approx p(y \vert x, \theta_{MP})$

덧붙여서 말하자면, 빈도론자들이 overfitting을 막기 위해 쓰는 regularization 기법(ex: L2-loss)가 사실 이 Poor Bayes와 본질적으로 동등하다.

Variational Inference

Main Goal: to estimate $p(\theta \vert x)$

그러면 conjugacy가 없고, 다시 말해 analytical하게 푸는 것이 불가능한 상황에서 우리는 어떻게 해야할까? 방법은 크게 두 가지로 나뉜다.

1. variational inference: $q(\theta) \approx p(\theta \vert x)$
2. sampling based method: $p(x \vert \theta)p(\theta)$로 부터 샘플링하는 방법. MCMC 등이 있으나 시간이 오래 걸린다.

우리는 여기서 첫 번째 방법인 variational inference에 대해 알아보려고 한다. approximate posterior를 가정하고, true posterior과 최대한 가깝게 approximate posterior를 추정하는 방법이다. 분포의 거리를 측정하기 위해 우리는 KL-divergence를 사용한다. KL-divergence는 워낙 유명한 토픽이고 서치하기도 쉬우니까 생략..

$\hat{q}(\theta) = argmin_{q}D_{KL}(q(\theta) \vert\vert p(\theta \vert x)) = argmin_{q} \int q(\theta)log\frac{q(\theta)}{p(\theta \vert x)}d\theta$

• 문제1: $p(\theta \vert x)$를 모른다.
• 문제2: 분포에 대한 optimization은 어떻게 할 수 있나?

Sol)

$logp(x) = E_{q(\theta)}[logp(x)] = \int q(\theta)logp(x)d\theta = \int q(\theta)log\frac{p(x, \theta)}{p(\theta \vert x)}d\theta= \int q(\theta)log\frac{p(x, \theta)}{p(\theta \vert x)}\frac{q(\theta)}{q(\theta)}d\theta$

$= \int q(\theta) log\frac{p(x, \theta)}{q(\theta)}d\theta + \int q(\theta) log\frac{q(\theta)}{p(\theta \vert x)}d\theta = \mathcal{L}(q(\theta)) + D_{KL}(q(\theta) \vert\vert p(\theta \vert x))$

따라서, $D_{KL}(q(\theta) \vert\vert p(\theta \vert x))$를 minimize하는 문제는 $\mathcal{L}(q(\theta))$를 maximize하는 문제와 동등해진다.

$\mathcal{L}(q(\theta)) = \int q(\theta) log\frac{p(x, \theta)}{q(\theta)}d\theta = \int q(\theta) log\frac{p(x \vert \theta)p(\theta)}{q(\theta)}d\theta$

$= E_{q(\theta)}[logp(x \vert \theta)] - D_{KL}(q(\theta) \vert\vert p(\theta)) = \text{data likelihood + KL-regularizer term}$

이제 남은 부분은 $q(\theta)$를 어떻게 최적화하는지인데, 크게 두 가지 방법이 있다.

1. mean field approximation: $\theta$끼리 독립일 때 사용하는 방법.
2. parametric approximation: 대부분의 neural network에서 사용하는 방법. $q(\theta)=q(\theta \vert \lambda)$라고 정의한 후 $\lambda$에 대해서 최적화.

지금까지 배운 것들을 요약해보자면 다음과 같다.

• Full Bayesian inference: $p(\theta \vert x)$
• MP inference: $\theta_{MP} = argmax_{\theta}p(\theta \vert X, Y)$
• Mean field variational inference: $p(\theta \vert x) \approx q(\theta) = \prod_{j=1}^{m}q_{j}(\theta_{j})$
• Parametric variational inference: $p(\theta \vert x) \approx q(\theta) = q(\theta \vert \lambda)$

Latent Variable Models

그럼 VAE를 배우기 전에 먼저 latent variable models에 대해서 짚고 넘어가자. variational inference에 대해서 신나게 공부하다가 갑자기 잠재변수모델이라니 조금 뜬금없어보이지만 VAE는 잠재변수 모델의 일종이기 때문에 반드시 짚고 넘어가야 한다.

왜 잠재변수를 학습해야하는가? 이미지 데이터를 예로 들어보자. RGB 채널을 갖는 32x32 짜리 이미지 데이터는 32x32x3 = 3072 차원을 갖는다. 그러나 통상적으로 생각해보았을때, 3072 차원을 통째로 다 feature로 쓰기 보다는 이미지를 결정하는 잠재변수가 있다고 보고 이를 바탕으로 추론을 하는 것이 타당하다.

예를 들어 MNIST 데이터에서 28x28=784개의 픽셀이 모두 의미있는 값이라고 보기보다는 숫자의 모양을 결정하는 변수(가장자리의 빈 정도, 선의 굽은 모양 등)가 있다고 보는 것이 맞다.

잠재변수 모델을 설명하는데 가장 흔하게 쓰이는 분포가정이 Mixture of Gaussians이다. 즉, 여러개의 가우시안 분포가 혼합되어 있는 분포로 아래 그림과 같다.앞서 말한 대한민국 평균 키로 설명해보자면, 우리나라 사람들의 키의 분포는 남성/여성/성인/아동 등 여러 분포로 나뉠 수 있다. (이미지 출처)

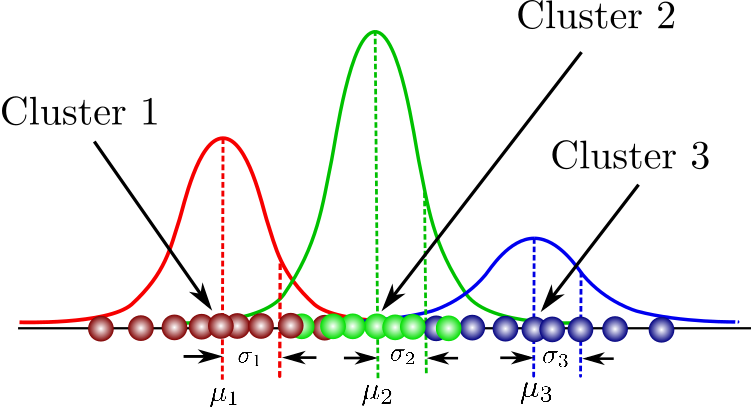
그럼 $i$번째 표본을 $x_{i}$라고 하고 그 표본이 속한 집단을 $z_{i}$(잠재변수)라고 해보자. 그러면 우리가 가진 데이터의 likelihood는 다음과 같이 나타낼 수 있다.

$p(X, Z \vert \theta)=\prod_{i=1}^{n}p(x_{i}, z_{i} \vert \theta) = \prod_{i=1}^{n}p(x_{i} \vert z_{i},\theta)p(z_{i} \vert \theta) = \prod_{i=1}^{n}\pi_{z_{i}} \mathcal{N}(x_{i} \vert \mu_{z_{i}}, \sigma_{z_{i}}^{2})$

여기서 $\pi_{j}=p(z_{i}=j)$로 $j$번째 그룹에 속할 확률을 의미하고 추정해야 할 파라미터는 $\theta = ( \mu_{j}, \sigma_{j}, \pi_{j} )_{j=1}^{K}$를 뜻한다.

만약 $X, Z$를 모두 안다면 $\hat{\theta} = argmax_{\theta}logP(X, Z \vert \theta)$로 쉽게 추정할 수 있겠지만 문제는 우리는 Z를 모른다는 것이다. 따라서 우리는 $X$의 log likelihood를 최대화하게 되고 목표식은 아래와 같다.

$logP(X \vert \theta)=\int q(Z)logP(X \vert \theta)dZ=\int q(Z) log \frac{P(X, Z \vert \theta)}{P(Z \vert \theta)} \frac{q(Z)}{q(Z)}dZ = \mathcal{L(q(Z))}+D_{KL}(q(Z) \vert\vert p(Z \vert \theta))$

항상 KL-divergence는 0 이상이므로 $logP(X \vert \theta)$의 lower-bound는 $\mathcal{L}(q(Z))$가 된다. 이를 Variational lower bound 또는 ELBO라고 칭한다. 결국, 우리는 이 하한값을 maximize하는 $q, \theta$를 찾는 것으로 목표를 바꾸게 된다. 결국, 잠재변수만 추가되었을 뿐 위에서 배운 variational inference와 완전히 똑같은 문제다!

이를 푸는 방법으로 EM 알고리즘이 존재한다. EM은 Expectation-Maximization의 약자로, 이름 그대로 Expectation step과 Maximization step이 있다.

1. E-step: $q(Z)$를 추론하는 과정으로, 이때 $\theta=\theta_{0}$으로 고정된다.
   $q(Z) = argmax_{q}\mathcal{L}(q, \theta_{0}) = argmin_{q}D_{KL}(q(z) \vert\vert p(z \vert \theta))=p(Z \vert X, \theta_{0})$
   자세히 풀어서 설명하자면 다음과 같다. $q(Z)$는 Multinomial 분포임을 기억하자.
   $q(z_{i}=k)=p(z_{i}=k \vert x, \theta) = \frac{p(x_{i} \vert k, \theta)p(z_{i}=k \vert \theta)}{\sum_{l=1}^{K}p(x_{i} \vert l, \theta)p(z_{i}=l \vert \theta)}$
2. M-step: $q(Z)$를 고정시켜놓고 $\theta$를 추론하는 과정이다.
   $\hat{\theta} = argmax_{\theta} \mathcal{L}(q, \theta) = argmax_{\theta} \mathbb{E_{Z}}[logp(X, Z \vert \theta)]=\sum_{i=1}^{n}\sum_{k=1}^{K}q(z_{i}=k)logp(x_{i}, k \vert \theta)$
3. repeat 1, 2 until convergence.

자, 여기서 드는 의문점이 있다. 위의 상황에서는 $Z$가 categorical variable이니까 단순합으로 E-step에서 $P(Z \vert X, \theta)$를 계산할 수 있다. 하지만 $Z$가 만약 continuous variable이라면? $p(x \vert z, \theta), p(z \vert \theta)$가 conjugate 하지 않다면 intractable 하게 된다!

continuous latent variable을 학습하는 것은 dimension reduction(차원축소) 또는 representation learning에 해당하고 사실 머신러닝에서 매우매우 중요하면서도 어려운 부분이다. 적분으로 인한 intractable 문제를 VAE에서는 어떻게 해결하는지 다음 섹션에서 알아보겠다.

Stochastic Variational Inference and VAE

우리는 지금까지 Bayesian framework를 이용한 variational inference와 latent variable model에 대해서 배웠다. 실제로 관측되지 않는 잠재변수를 모델링하기 위해 variational inference를 사용($q(Z)$를 추론)해 학습을 진행하는 방법이었다. 하지만 사후분포를 추론할 때 처럼 잠재변수 $Z$가 continuous 하다면 intractability 문제에 직면하게 된다. 앞서 잠깐 언급한 바와 같이 이 문제를 해결하기 위해 여러 sampling 방법들이 고안되었다. 하지만 역시 시간이 많이 걸린다. 또한 Monte Carlo로 추정한 gradient는 분산이 매우 커진다고 한다. 이런 한계점을 극복하기 위해 VAE는 reparameterization trick을 이용하였고, end-to-end learning이 가능해졌다!

즉, 우리의 목표는 두 가지다.

1. Generation을 제대로 할 것 => $logP(X)$를 maximize하는 목표
2. Latent variable Z의 분포를 제대로 학습할 것 => $q(Z \vert X) \approx p(Z \vert X)$

먼저, 첫 번째 목표를 이루기 위해 $logP(X)$를 풀어쓰면 다음과 같다. (이미지 출처)

지금까지와 같이, 맨 마지막 KL-term을 제외한 나머지 것들이 lower bound가 된다. 결국, $logP(X)$를 최대화하는 목표는 lower bound를 최대화하는 목표로 바뀌고 이는 동시에 두 번째 목표까지 이루게 된다! lower bound 식은 아래와 같다.

$\mathcal{L}(\theta, \phi; x^{(i)}) = D_{KL}(q(z \vert x^{(i)}) \vert\vert p(z))+\mathbb{E_{q(z \vert x^{(i)})}}[logp(x^{(i)} \vert z)]$

앞부분은 prior과 approximate posterior와의 KL term이고, 뒷부분은 decoder probability에 해당한다. 대부분 잠재변수 Z의 prior 분포를 $\mathcal{N}[0, 1]$와 같은 다루기 쉬운 분포로 정한다. 그러면 $q(z \vert x)$는 어떻게 정의했을까? VAE original paper에서는 다변량 정규분포로 정의하는데, 다음과 같다.

$q(z_{i} \vert x_{i}, \phi) = \prod_{j=1}^{d}\mathcal{N}[\mu_{j}(x_{i}), \sigma_{j}^{2}(x_{i})]$

이때 $\mu_{j}(x_{i}), \sigma_{j}^{2}(x_{i})$는 $x_{i}$가 DNN을 통과한 output에 해당한다. 그래서 구현된 코드를 보면 알겠지만, VAE의 encoder에서는 $\mu_{j}(x_{i}), \sigma_{j}^{2}(x_{i})$를 구한다. 그러면 $p(z), q(z \vert x)$의 KL-divergence를 구할 수 있게 된다. (둘 다 정규분포이므로) 사실 이 term은 approximate posterior가 prior와 너무 달라지지 않게 하는 regularizer 역할을 해준다.

decoder probability에 해당하는 뒷부분을 보면 $q(z \vert x)$에 기반하여 $log(x \vert z)$의 평균을 구해야 한다. 바로 여기서 intractability에 직면한다. 앞서 말했다시피 Monte Carlo 방법으로 평균을 추정하게 되면 gradient의 분산이 매우 커지는 동시에 수렴할 때까지 시간이 오래걸리는 문제가 있다. 게다가 무엇보다도, sampling은 미분가능한 연산이 아니기 때문에 역전파로 학습할 수가 없게 된다. VAE의 저자들을 똑똑하게도, reparameterization trick을 이용했다.

사실 이 수식이 reparam trick의 전부인데, 처음에는 수식만 보고 읭?했었다. 그런데 회귀분석의 문제로 이해하면 쉬운 문제다.

간단하게 언급하자면, $y$변수(타겟변수)가 $x$변수(feature)와 linear한 관계에 있다고 가정하고 $y = ax+b+\epsilon$식에서 $a, b$를 푸는 것인데 결국 이는 $p(y \vert x)$를 구하는 태스크가되고 $x$는 given, $a, b$는 constant라고 가정하기 때문에 random factor은 $\epsilon$ ~ $N(0, 1)$에서만 생긴다. 즉, $p(y \vert x)$는 $ax+b$를 평균으로하고 1을 분산으로 하는 정규분포가 된다. 따라서 $a, b$는 MLE 방법으로 closed-form solution이 나오게 된다. 지금까지 설명한 VAE와 개념적으로 상당히 비슷함을 알 수 있다.

결국 $g(\epsilon, x)$는 본인은 deterministic한 function인데 외부에서 noise $\epsilon$이 들어왔다고 이해하게 되고, 미분이 가능해진다. end-to-end learning이 가능해지는 것이다!

마지막으로 VAE의 단점인 blurry generation을 짚고 넘어가려고한다. approximate posterior가 regularizer 역할을 하고, reconstruction loss가 실제 cost에 해당한다고 볼 수 있기 때문에 $logp(x \vert z)$를 높이는 방향으로 학습이 된다. 이는 일종의 Linear Regression(MLE)으로 볼 수 있고, 결국 $x$의 평균과 가까워지게 된다. 따라서 VAE로 생성된 이미지는 보다 흐리다.

VAE로 학습된 Z를 통해 이미지를 생성한 결과는 다음과 같다. (이미지 출처)

D=2인 Z축에서 매우 smooth하게 변하고 있음을 볼 수 있다.

Conclusion

이번 포스팅에서는 Bayesian의 중요한 토픽인 Variational Inference부터 그와 연관된 Variational Auto-encoder까지 알아보았다. intractible posterior를 estimate하기 위한 기법 중의 하나가 Variational Inference였고 EM 알고리즘 등을 통해 잠재변수 모델에 활용됨을 알 수 있었다. VAE는 이를 활용한 생성모델+잠재변수 모델로 보다 시각화/설명이 용이하지만 흐린 이미지를 생성한다는 것까지 살펴보았다. 앞으로도 representation learning의 중요성은 더 부각될 것 같다. 열심히 공부해야지..